Publications
Reduced-Order Shape Optimization Using Offset Surfaces
Proceedings of the 2015 SIGGRAPH Conference
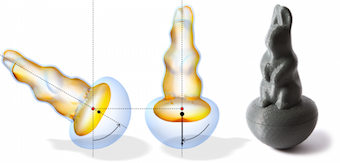
Given the 2-manifold surface of a 3d object, we propose a novel method for the computation of an offset surface with varying thickness such that the solid volume between the surface an its offset satisfies a set of prescribed constraints and at the same time minimizes a given objective functional. Since the constraints as well as the objective functional can easily be adjusted to specific application requirements, our method provides a flexible and powerful tool for shape optimization. We use manifold harmonics to derive a reduced-order formulation of the optimization problem which guarantees a smooth offset surface and speeds up the computation independently from the input mesh resolution without affecting the quality of the result. The constrained optimization problem can be solved in a numerically robust manner with commodity solvers. Furthermore, the method allows to simultaneously optimize an inner and an outer offset in order to increase the degrees of freedom. We demonstrate our method in a number of examples where we control the physical mass properties of rigid objects for the purpose of 3d printing.
» Show BibTeX
@article{musialski-2015-souos,
title = "Reduced-Order Shape Optimization Using Offset Surfaces",
author = "Przemyslaw Musialski and Thomas Auzinger and Michael Birsak
and Michael Wimmer and Leif Kobbelt",
year = "2015",
abstract = "Given the 2-manifold surface of a 3d object, we propose a
novel method for the computation of an offset surface with
varying thickness such that the solid volume between the
surface an its offset satisfies a set of prescribed
constraints and at the same time minimizes a given objective
functional. Since the constraints as well as the objective
functional can easily be adjusted to specific application
requirements, our method provides a flexible and powerful
tool for shape optimization. We use manifold harmonics to
derive a reduced-order formulation of the optimization
problem which guarantees a smooth offset surface and speeds
up the computation independently from the input mesh
resolution without affecting the quality of the result. The
constrained optimization problem can be solved in a
numerically robust manner with commodity solvers.
Furthermore, the method allows to simultaneously optimize an
inner and an outer offset in order to increase the degrees
of freedom. We demonstrate our method in a number of
examples where we control the physical mass properties of
rigid objects for the purpose of 3d printing.",
pages = "to appear--9",
month = aug,
number = "4",
event = "ACM SIGGRAPH 2015",
journal = "ACM Transactions on Graphics (ACM SIGGRAPH 2015)",
volume = "34",
location = "Los Angeles, CA, USA",
keywords = "reduced-order models, shape optimization, computational
geometry, geometry processing, physical mass properties",
URL = "http://www.cg.tuwien.ac.at/research/publications/2015/musialski-2015-souos/",
}
BendFields: Regularized Curvature Fields from Rough Concept Sketches
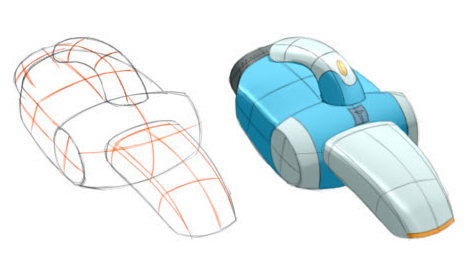
Designers frequently draw curvature lines to convey bending of smooth surfaces in concept sketches. We present a method to extrapolate curvature lines in a rough concept sketch, recovering the intended 3D curvature field and surface normal at each pixel of the sketch. This 3D information allows to enrich the sketch with 3D-looking shading and texturing. We first introduce the concept of regularized curvature lines that model the lines designers draw over curved surfaces, encompassing curvature lines and their extension as geodesics over flat or umbilical regions. We build on this concept to define the orthogonal cross field that assigns two regularized curvature lines to each point of a 3D surface. Our algorithm first estimates the projection of this cross field in the drawing, which is nonorthogonal due to foreshortening. We formulate this estimation as a scattered interpolation of the strokes drawn in the sketch, which makes our method robust to sketchy lines that are typical for design sketches. Our interpolation relies on a novel smoothness energy that we derive from our definition of regularized curvature lines. Optimizing this energy subject to the stroke constraints produces a dense nonorthogonal 2D cross field which we then lift to 3D by imposing orthogonality. Thus, one central concept of our approach is the generalization of existing cross field algorithms to the nonorthogonal case. We demonstrate our algorithm on a variety of concept sketches with various levels of sketchiness. We also compare our approach with existing work that takes clean vector drawings as input.
» Show BibTeX
@Article{IBB15,
author = "Iarussi, Emmanuel and Bommes, David and Bousseau, Adrien",
title = "BendFields: Regularized Curvature Fields from Rough Concept Sketches ",
journal = "ACM Transactions on Graphics",
year = "2015",
url = "http://www-sop.inria.fr/reves/Basilic/2015/IBB15"
}
Quantized Global Parametrization
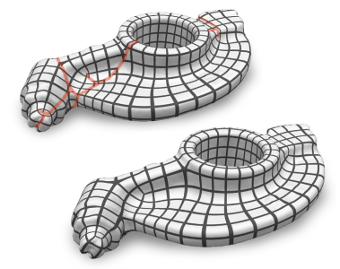
Global surface parametrization often requires the use of cuts or charts due to non-trivial topology. In recent years a focus has been on so-called seamless parametrizations, where the transition functions across the cuts are rigid transformations with a rotation about some multiple of 90 degrees. Of particular interest, e.g. for quadrilateral meshing, paneling, or texturing, are those instances where in addition the translational part of these transitions is integral (or more generally: quantized). We show that finding not even the optimal, but just an arbitrary valid quantization (one that does not imply parametric degeneracies), is a complex combinatorial problem. We present a novel method that allows us to solve it, i.e. to find valid as well as good quality quantizations. It is based on an original approach to quickly construct solutions to linear Diophantine equation systems, exploiting the specific geometric nature of the parametrization problem. We thereby largely outperform the state-of-the-art, sometimes by several orders of magnitude.
Data Driven 3D Face Tracking Based on a Facial Deformation Model

We introduce a new markerless 3D face tracking approach for 2D video streams captured by a single consumer grade camera. Our approach is based on tracking 2D features in the video and matching them with the projection of the corresponding feature points of a deformable 3D model. By this we estimate the initial shape and pose of the face. To make the tracking and reconstruction more robust we add a smoothness prior for pose changes as well as for deformations of the faces. Our major contribution lies in the formulation of the smooth deformation prior which we derive from a large database of previously captured facial animations showing different (dynamic) facial expressions of a fairly large number of subjects. We split these animation sequences into snippets of fixed length which we use to predict the facial motion based on previous frames. In order to keep the deformation model compact and independent from the individual physiognomy, we represent it by deformation gradients (instead of vertex positions) and apply a principal component analysis in deformation gradient space to extract the major modes of facial deformation. Since the facial deformation is optimized during tracking, it is particularly easy to apply them to other physiognomies and thereby re-target the facial expressions. We demonstrate the effectiveness of our technique on a number of examples.
VMV 2015 Honorable Mention
ACTUI: Using Commodity Mobile Devices to Build Active Tangible User Interfaces
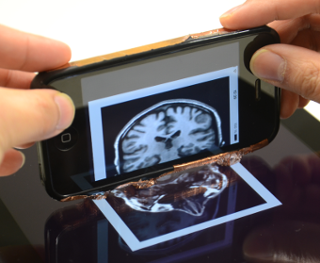
We present the prototype design for a novel user interface, which extends the concept of tangible user interfaces from mostly specialized hardware components and studio deployment to commodity mobile devices in daily life. Our prototype enables mobile devices to be components of a tangible interface where each device can serve as both, a touch sensing display and as a tangible item for interaction. The only necessary modification is the attachment of a conductive 2D touch pattern on each device. Compared to existing approaches, our Active Commodity Tangible User Interfaces (ACTUI) can display graphical output directly on their built-in display paving the way to a plethora of innovative applications where the diverse combination of local and global active display area can significantly enhance the flexibility and effectiveness of the interaction. We explore two exemplary application scenarios where we demonstrate the potential of ACTUI.
Active Exploration of Large 3D Model Repositories

With broader availability of large-scale 3D model repositories, the need for efficient and effective exploration becomes more and more urgent. Existing model retrieval techniques do not scale well with the size of the database since often a large number of very similar objects are returned for a query, and the possibilities to refine the search are quite limited. We propose an interactive approach where the user feeds an active learning procedure by labeling either entire models or parts of them as “like” or “dislike” such that the system can automatically update an active set of recommended models. To provide an intuitive user interface, candidate models are presented based on their estimated relevance for the current query. From the methodological point of view, our main contribution is to exploit not only the similarity between a query and the database models but also the similarities among the database models themselves. We achieve this by an offline pre-processing stage, where global and local shape descriptors are computed for each model and a sparse distance metric is derived that can be evaluated efficiently even for very large databases. We demonstrate the effectiveness of our method by interactively exploring a repository containing over 100K models.
» Show BibTeX
@ARTICLE{6951464,
author={L. {Gao} and Y. {Cao} and Y. {Lai} and H. {Huang} and L. {Kobbelt} and S. {Hu}},
journal={IEEE Transactions on Visualization and Computer Graphics},
title={Active Exploration of Large 3D Model Repositories},
year={2015},
volume={21},
number={12},
pages={1390-1402},}
Nonparametric Facial Feature Localization Using Segment-Based Eigenfeatures
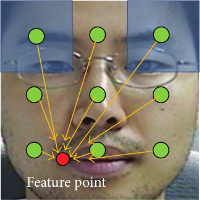
We present a nonparametric facial feature localization method using relative directional information between regularly sampled image segments and facial feature points. Instead of using any iterative parameter optimization technique or search algorithm, our method finds the location of facial feature points by using a weighted concentration of the directional vectors originating from the image segments pointing to the expected facial feature positions. Each directional vector is calculated by linear combination of eigendirectional vectors which are obtained by a principal component analysis of training facial segments in feature space of histogram of oriented gradient (HOG). Our method finds facial feature points very fast and accurately, since it utilizes statistical reasoning from all the training data without need to extract local patterns at the estimated positions of facial features, any iterative parameter optimization algorithm, and any search algorithm. In addition, we can reduce the storage size for the trained model by controlling the energy preserving level of HOG pattern space.
Influence of Temporal Delay and Display Update Rate in an Augmented Reality Application Scenario

In mobile augmented reality (AR) applications, highly complex computing tasks such as position tracking and 3D rendering compete for limited processing resources. This leads to unavoidable system latency in the form of temporal delay and reduced display update rates. In this paper we present a user study on the influence of these system parameters in an AR point'n'click scenario. Our experiment was conducted in a lab environment to collect quantitative data (user performance as well as user perceived ease of use). We can show that temporal delay and update rate both affect user performance and experience but that users are much more sensitive to longer temporal delay than to lower update rates. Moreover, we found that the effects of temporal delay and update rate are not independent as with longer temporal delay, changing update rates tend to have less impact on the ease of use. Furthermore, in some cases user performance can actually increase when reducing the update rate in order to make it compatible to the latency. Our findings indicate that in the development of mobile AR applications, more emphasis should be put on delay reduction than on update rate improvement and that increasing the update rate does not necessarily improve user performance and experience if the temporal delay is significantly higher than the update interval.
@inproceedings{Li:2015:ITD:2836041.2836070,
author = {Li, Ming and Arning, Katrin and Vervier, Luisa and Ziefle, Martina and Kobbelt, Leif},
title = {Influence of Temporal Delay and Display Update Rate in an Augmented Reality Application Scenario},
booktitle = {Proceedings of the 14th International Conference on Mobile and Ubiquitous Multimedia},
series = {MUM '15},
year = {2015},
isbn = {978-1-4503-3605-5},
location = {Linz, Austria},
pages = {278--286},
numpages = {9},
url = {http://doi.acm.org/10.1145/2836041.2836070},
doi = {10.1145/2836041.2836070},
acmid = {2836070},
publisher = {ACM},
address = {New York, NY, USA},
keywords = {display update rate, ease of use, latency, mobile augmented reality, perception tolerance, point'n'click, temporal delay, user study},
}
Imalytics Preclinical: Interactive Analysis of Biomedical Volume Data
A software tool is presented for interactive segmentation of volumetric medical data sets. To allow interactive processing of large data sets, segmentation operations, and rendering are GPU-accelerated. Special adjustments are provided to overcome GPU-imposed constraints such as limited memory and host-device bandwidth. A general and efficient undo/redo mechanism is implemented using GPU-accelerated compression of the multiclass segmentation state. A broadly applicable set of interactive segmentation operations is provided which can be combined to solve the quantification task of many types of imaging studies. A fully GPU-accelerated ray casting method for multiclass segmentation rendering is implemented which is well-balanced with respect to delay, frame rate, worst-case memory consumption, scalability, and image quality. Performance of segmentation operations and rendering are measured using high resolution example data sets showing that GPU-acceleration greatly improves the performance. Compared to a reference marching cubes implementation, the rendering was found to be superior with respect to rendering delay and worst-case memory consumption while providing sufficiently high frame rates for interactive visualization and comparable image quality.
Previous Year (2014)

